Sistemi numerici e termini

Tre principali aree di differenza dai nostri numeri

Immagina quanto sarebbe più facile imparare l'aritmetica nei primi anni se tutto ciò che dovevi fare fosse imparare a scrivere una riga come me e un triangolo. Questo è fondamentalmente tutto ciò che gli antichi popoli della Mesopotamia dovevano fare, anche se li variavano qua e là, allungandosi, girandosi, ecc.

Non avevano le nostre penne e matite, o carta per quella materia. Ciò con cui scrissero era uno strumento che si sarebbe usato nella scultura, dato che il mezzo era l'argilla. Se questo è più difficile o più facile da imparare rispetto a una matita è un gioco da ragazzi, ma finora sono avanti nel reparto facilità, con solo due simboli di base da imparare.

Il passo successivo lancia una chiave inglese nel reparto semplicità. Usiamo a Base 10, un concetto che sembra ovvio poiché abbiamo 10 cifre. In realtà ne abbiamo 20, ma supponiamo di indossare sandali con protezioni protettive per tenere lontana la sabbia il deserto, caldo dello stesso sole che cuocerebbe le tavolette di argilla e le conserverebbe per noi da trovare millenni dopo. I babilonesi usarono questa Base 10, ma solo in parte. In parte hanno usato Base 60, lo stesso numero che vediamo intorno a noi in minuti, secondi e gradi di un triangolo o cerchio. Erano astronomi affermati e quindi il numero poteva derivare dalle loro osservazioni sui cieli. Base 60 ha anche vari fattori utili che lo rendono facile da calcolare. Tuttavia, dover imparare la Base 60 è intimidatorio.

In "Omaggio a Babilonia" [La gazzetta matematica, Vol. 76, n. 475, "L'uso della storia della matematica nell'insegnamento della matematica" (marzo 1992), pagg. 158-178], lo scrittore-insegnante Nick Mackinnon afferma di usare la matematica babilonese per insegnare a tredicenni su basi diverse da 10. Il sistema babilonese utilizza la base 60, il che significa che invece di essere decimale, è sessagesimale.

Sia il nostro sistema numerico babilonese che il nostro si basano sulla posizione per dare valore. I due sistemi lo fanno diversamente, in parte perché il loro sistema mancava di zero. L'apprendimento del sistema posizionale babilonese da sinistra a destra (dall'alto verso il basso) per il primo assaggio dell'aritmetica di base non è probabilmente più difficile che apprendere il nostro bidirezionale, dove dobbiamo ricordare l'ordine dei numeri decimali - aumentando dal decimale, uno, decine, centinaia, e poi sventolando nell'altra direzione dall'altra parte, nessuna colonna, solo decimi, centesimi, millesimi, ecc.

Entrerò nelle posizioni del sistema babilonese in ulteriori pagine, ma prima ci sono alcune importanti parole numeriche da imparare.

Parliamo di periodi di anni usando quantità decimali. Abbiamo un decennio per 10 anni, un secolo per 100 anni (10 decenni) o 10X10 = 10 anni quadrati e un millennio per 1000 anni (10 secoli) o 10X100 = 10 anni al cubo. Non conosco termini più alti di quello, ma quelle non sono le unità utilizzate dai babilonesi. Nick Mackinnon fa riferimento a una tavoletta di Senkareh (Larsa) di Sir Henry Rawlinson (1810-1895) * per le unità utilizzate dai babilonesi e non solo per gli anni in questione, ma anche per le quantità implicite:

1. soss
2. ner
3. sar.

sossnersosssarsoss

Ancora nessun pareggio: non è necessariamente più facile imparare i termini dell'anno al quadrato e al cubo derivati dal latino di quanto non lo siano quelli babilonesi a una sillaba che non implicano il cubing, ma la moltiplicazione per 10.

Cosa pensi? Sarebbe stato più difficile imparare le basi del numero come un bambino di scuola babilonese o come uno studente moderno in una scuola di lingua inglese?

* George Rawlinson (1812-1902), il fratello di Henry, mostra una tavola trascritta di quadrati semplificata Le sette grandi monarchie dell'antico mondo orientale. La tabella sembra essere astronomica, basata sulle categorie degli anni babilonesi.

Tutte le foto provengono da questa versione digitalizzata online di un'edizione del XIX secolo di George Rawlinson Le sette grandi monarchie dell'antico mondo orientale.

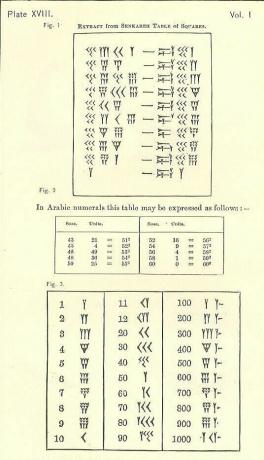
Da quando siamo cresciuti con un sistema diverso, i numeri babilonesi sono confusi.

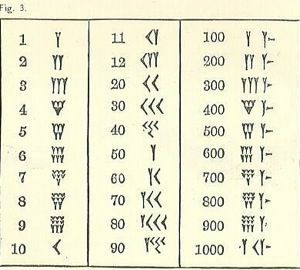
Almeno i numeri vanno dall'alto in alto a sinistra in basso a destra, come il nostro sistema arabo, ma il resto sembrerà probabilmente sconosciuto. Il simbolo di uno è un cuneo o una forma a Y. Sfortunatamente, la Y rappresenta anche un 50. Ci sono alcuni simboli separati (tutti basati sul cuneo e sulla linea), ma tutti gli altri numeri sono formati da essi.

Ricorda che la forma di scrittura è cuneiforme o a forma di cuneo. A causa dello strumento utilizzato per disegnare le linee, esiste una varietà limitata. Il cuneo può o meno avere una coda, disegnata tirando lo stilo per scrittura cuneiforme lungo l'argilla dopo aver impresso la forma del triangolo della parte.

Il 10, descritto come una punta di freccia, sembra un po 'come

Tre file fino a 3 piccoli 1 (scritti come Y con alcune code abbreviate) o 10 (un 10 è scritto come

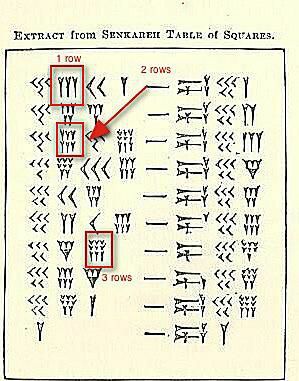
Esistono tre serie di numeri cuneiformi cluster evidenziato nell'illustrazione sopra.

In questo momento, non ci preoccupiamo del loro valore, ma della dimostrazione di come vedresti (o scriveresti) ovunque da 4 a 9 dello stesso numero raggruppati insieme. Tre vanno di fila. Se c'è un quarto, quinto o sesto, va sotto. Se c'è un settimo, ottavo o nono, hai bisogno di una terza fila.

Le pagine seguenti continuano con le istruzioni per eseguire calcoli con il cuneiforme babilonese.

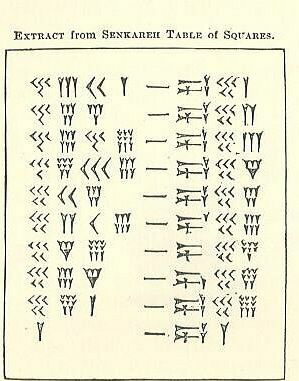
Da quello che hai letto sopra sul soss - che ricorderete è il babilonese per 60 anni, il cuneo e la punta di freccia - che sono nomi descrittivi per i segni cuneiformi, vedete se riuscite a capire come funzionano questi calcoli. Un lato del segno a forma di trattino è il numero e l'altro è il quadrato. Provalo come gruppo. Se non riesci a capirlo, guarda il passaggio successivo.

Riesci a capirlo ora? Dagli Una possibilità.

...

Ci sono 4 colonne chiare sul lato sinistro seguite da un segno simile a un trattino e 3 colonne sulla destra. Osservando il lato sinistro, l'equivalente della colonna 1s è in realtà le 2 colonne più vicine al "trattino" (colonne interne). Le altre 2 colonne esterne vengono conteggiate insieme come la colonna degli anni '60.

• Il 4-
• Il 3-Ys = 3.
• 40+3=43.
• L'unico problema qui è che c'è un altro numero dopo di loro. Ciò significa che non sono unità (il posto di quelle). Il 43 non è 43-uno ma 43-60, poiché è il sistema sessagesimale (base-60) ed è nel soss colonna come indica la tabella inferiore.
• Moltiplica 43 per 60 per ottenere 2580.
• Aggiungi il prossimo numero (2-
• Ora hai 2601.
• Questo è il quadrato di 51.

La riga successiva ha 45 in soss colonna, quindi moltiplichi 45 per 60 (o 2700), quindi aggiungi 4 dalla colonna unità, in modo da avere 2704. La radice quadrata di 2704 è 52.

Riesci a capire perché l'ultimo numero = 3600 (60 quadrati)? Suggerimento: perché non è 3000?